Heteroskedasticity is a name provided to a problem that arises when a set of data violates the assumption of which the disturbances all have the same variance. However, not all data within the data set have the same sizes in a data set. The variance is connected to the of which the error term will vary directly according to the size. If the variance is constant , then the condition is homoskedasticity, but if the variance is not constant, then the condition is called heteroskedasticity.
As represented in the diagram above, there are four graphs, both the bottom right corner and top left corner shows heteroskedasticity, whereas the remaining two graphs depicts homoskedasticity.
In the heteroskedasticity 2 graphs, the errors grow larger as X approaches some value of X and then will diminished thereafter. Here, a systematic relationship between the errors and the size of X violates the assumption. As for homoskedasticity, if the error term continuously grows, then X will too also continue to grow.
Within heteroskedasticity conditions, some variances are larger than others, however, if all variances were of equal size and weight, then the variances will be overweight in their importance. This subsequently means, although the variance have a mean of zero and are normally distributed. the ordinary square estimator will no longer be the best estimator. It will still be linear and unbiased - the assumptions here will not be altered nor would it be the best one and therefore cannot state this as BLUE (Best Linear Unbiased Estimator)
Subsequently, the best way forward, can be found by applying weights in order to determine some sort of importance of the error terms. The intention here is to bring the overweight variances back in line to help satisfy the required assumption. This procedure is namely called, ordinary least squares in a generalised least square (GLS). A GLS estimator is considered to have a smaller variance than an OLS and is percieved as the best and is called as a BLUE (Unbiased Estimator). This is another 'best' one and is the most 'efficient' one.
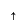
"The variance is connected to the [missing word] of which the error term will vary directly according to the size."
ReplyDelete